三角函数在高中时就已经学过,不过相信不少小伙伴已经把这些知识还给数学老师了。没关系,现在我来带大家慢慢捡起来,以后你们还给我就行。
在Math对象中,用于三角函数操作的常用方法如下表所示。
| 方法 | 说明 |
|---|---|
| sin(x) | 正弦 |
| cos(x) | 余弦 |
| tan(x) | 正切 |
| asin(x) | 反正弦 |
| acos(x) | 反余弦 |
| atan(x) | 反正切 |
| atan2(y, x) | 反正切(注意y、x顺序) |
x表示角度值,用弧度来表示,常用形式为度数*Math.PI/180,这一点我们之前说过了。对于上表的三角函数方法,有2点需要跟大家说明一下的。
- (1)atan2(y, x)跟atan(x)是不一样的,atan2(y, x)能够精确判断角度对应哪一个角,而atan(x)不能。因此在高级动画开发时,我们大多数用的是atan2(y, x),基本用不到atan(x)。
- (2)反三角函数用得很少(除了atan2()),一般都是用三角函数,常用的有:sin()、cos()和atan2()。
举例:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8" />
<title></title>
<script>
document.write("sin30°:" + Math.sin(30 * Math.PI / 180) + "<br/>");
document.write("cos60°:" + Math.cos(60 * Math.PI / 180) + "<br/>");
document.write("tan45°:" + Math.tan(45 * Math.PI / 180));
</script>
</head>
<body>
</body>
</html>
浏览器预览效果如下图所示。
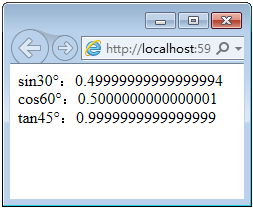
分析:
咦,sin30°不是等于0.5么?为什么会出现上面这种结果呢?其实,这是因为JavaScript计算会有一定的精度,但是误差非常小,可以忽略不计。
那到底这些三角函数有啥用啊?!现在我们是用不上的,不过这些却是高级动画开发的基础。就像你学数学,不都是一开始先学一下运算公式,然后到后面才知道用在哪些地方的嘛。当然这本书只是仅仅是带大家入门而已,对于三角函数在动画开发中的具体应用,可以看看本系列图书中的《从0到1:HTML5 Canvas动画开发》。
